
1.“I have not yet decided what I will do this evening; I ______ visit a friend.”
(a) mite
(b) would
(c) might
(d) didn’t
Sol: (c)
Let’s understand the meaning of each option:
A.“Mite”: It is a noun referring to a tiny arachnid, not a verb expressing uncertainty.
B.“Would”: It is a modal verb used for hypothetical situations or polite requests, not uncertainty about future plSol:
C.“Might”: It is a modal verb indicating possibility or uncertainty about a future action, fitting the context of the sentence.
D.“Didn’t”: It is the past tense of “do not” or “did not,” not suitable for expressing uncertainty about future plSol:
Answer:– I might visit a friend
2. Eject: Insert: : Advance : ______ (By word meaning)
(a) Advent
(b) Progress
(c) Retreat
(d) Loan
Sol: (c)
In this analogy, the relationship between the words is based on their meanings:
“Eject” means to expel or force something out.
“Insert” means to put something in or introduce it into something else.
The relationship between the words in the given analogy is that they represent opposite actions.
Now let’s understand each option.
“Advent” means the arrival or the coming of something, which is not the opposite of “Advance.”
“Progress” is not the opposite of “Advance”, as progress implies moving forward towards a goal.
“Retreat” is the correct option to complete the analogy.
“Loan” is not related to the given pair of words and doesn’t fit the analogy.
Therefore, the word that is the opposite of “Advance” is retreat
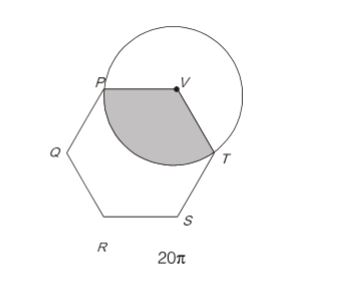
3. In the given figure, PQRSTV is a regular hexagon with each side of length 5 cm. A circle is drawn with its centre at V such that it passes through P. What is the area (in cm2 ) of the shaded region? (The diagram is representative)
(a) 25/3 π
(b) 20/3 π
(c) 6 π
(d) 7π
Sol: (a)
Sum of interior angles of any polygon = (n – 2) × 180° = (6 – 2) × 180° = 720°
Each interior angle=θ= 7206=120⁰
Now, required sector area =360R2=120360π×52=25π3
4.A duck named Donald Duck says “All ducks always lie.” Based only on the information above, which one of the following statements can be logically inferred with certainty?
(a) Donald Duck always lies.
(b) Donald Duck always tells the truth
(c) Donald Duck’s statement is true.
(d) Donald Duck’s statement is false.
Sol: (d)
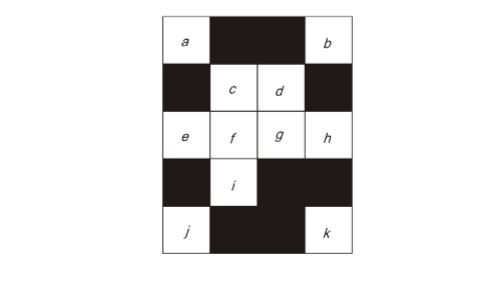
5.A line of symmetry is defined as a line that divides a figure into two parts in a way such that each part is a mirror image of the other part about that line. The figure below consists of 20 unit squares arranged as shown. In addition to the given black squares, upto 5 more may be coloured black. Which one among the following options depicts the minimum number of boxes that must be coloured black to achieve two lines of symmetry? (The figure is representative)
(a) d
(b) c, d, i
(c) c, i
(d) c, d, i, f, g
Sol: (b)
if box d or I is coloured block we get one line of symmetry, i.e., horizontal or vertical. But for two lines of symmetry, we need to atleast colour 3 box, i.e., c, d and i.
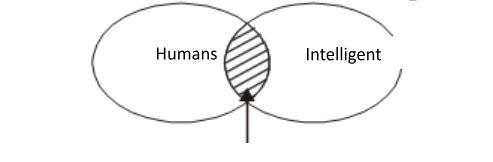
6.Based only on the truth of the statement ‘Some humans are intelligent’, which one of the following options can be logically inferred with certainty?
(a) No human is intelligent.
(b) All humans are intelligent.
(c) Some non-humans are intelligent.
(d) Some intelligent beings are humSol:
Sol: (d)
- “Some humans are intelligent” can be represented by Venn diagram.
- “Some human’s are intelligent” can be also represented by Venn-Diagram.
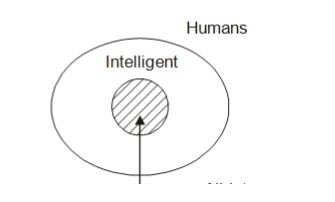
Being are human is correct so some intelligent beings are human is also correct. Hence, option (d) can be logically correct. Option (c) some non humans are intelligent is a possibility only which true in (1) diagram but false in (2).
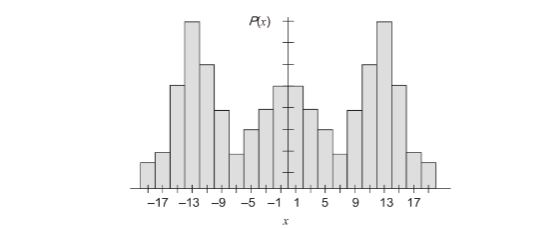
7. Which one of the options can be inferred about the mean, median, and mode for the given probability distribution (i.e. probability mass function), (𝑥), of a variable x?
(a) mean = median ≠ mode
(b) mean = median = mode
(c) mean ≠ median = mode
(d) mean ≠ mode = median
Sol: (a)
Median=–1+12=0
Mode= -13,13 (Date with high probability)
So median mode
8.The James Webb telescope, recently launched in space, is giving humankind unprecedented access to the depths of time by imaging very old stars formed almost 13 billion years ago. Astrophysicists and cosmologists believe that this odyssey in space may even shed light on the existence of dark matter. Dark matter is supposed to interact only via the gravitational interaction and not through the electromagnetic-, the weak- or the strong-interaction. This may justify the epithet “dark” in dark matter. Based on the above paragraph, which one of the following statements is FALSE?
(a) No other telescope has captured images of stars older than those captured by the James Webb telescope.
(b) People other than astrophysicists and cosmologists may also believe in the existence of dark matter.
(c) The James Webb telescope could be of use in the research on dark matter.
(d) If dark matter was known to interact via the strong-interaction, then the epithet “dark” would be justified
Sol: (d)
9. Let a = 30!, b = 50!, and c = 100!;. Consider the following numbers: logac, logca, logba , loga b
Which one of the following inequalities is CORRECT?
(a) logca<logba<logab<logac
(b) logca<logbb<logba<logbc
(c) logca<logba<logac<logab
(d) logba<logca<logab<logac
Sol: (a)
Given, a = 30!, b = 50!, and c = 100!
logaC=log C log a =log 100! log 30!
So logaC is greatest one.
logca=log a log c =log 30! log 100!
So, logca is smallest one.
So
logba=log a log c =log 30! log 50!
logab=log b log a =log 50! log 30!
logba<1 and logab>1. So logab>logba
log 30! log 100! < log 30! log 50! < log 50! log 30! < log 100! log 30!
Hence, option (a) is correct.
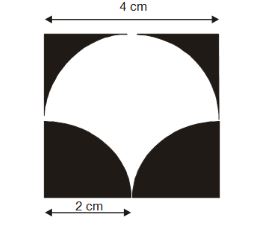
10.A square of side length 4 cm is given. The boundary of the shaded region is defined by one semi-circle on the top and two circular arcs at the bottom, each of radius 2 cm, as shown. The area of the shaded region is _____cm2 .
(a) 8
(b) 4
(c) 12
(d) 10
Sol: (a)
Top shaded area = 42–222=8–2
- Bottom shaded area = 2242=2
Total shaded area = 8-2+2=8
Q.11 – Q.35 carry ONE mark each
- For the integral
I=–111X2dx
which of the following statements is TRUE?
(a) I = 0
(b) I = 2
(c) I = – 2
(d) The integral does not converge
Sol: (d)
I=–111X2dx=2011x2dx (f(-x)=f(x))
=2limt0+ –1xt1 =-2limt0+1-1t
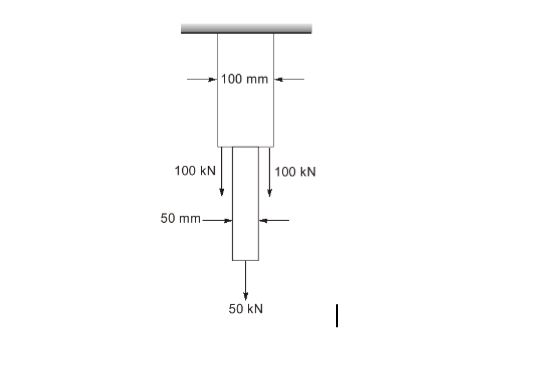
= 2-1 = ∝
12.A hanger is made of two bars of different sizes. Each bar has a square cross-section. The hanger is loaded by three-point loads in the mid vertical plane as shown in the figure. Ignore the self-weight of the hanger. What is the maximum tensile stress in N/mm2 anywhere in the hanger without considering stress concentration effects?
(a) 15.0
(b) 25.0
(c) 35.0
(d) 45.0
Sol: (b)
FBD
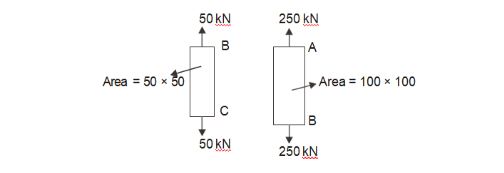
Stress at AB= PABAAB= 250103100100=25N/mm2
Stress at BC= PBCABC= 501035050=20 N/mm2
Maximum stress = Stress at AB= 25N/mm2
13.Creep of concrete under compression is defined as the ______
(a) increase in the magnitude of strain under constant stress
(b) increase in the magnitude of stress under constant strain
(c) decrease in the magnitude of strain under constant stress
(d) decrease in the magnitude of stress under constant strain
Sol: (a)
Under sustained compressive loading, deformation in concrete increases with time even through the applied stress level is not changed. The time dependent component of strain is called creep. Hence, correct answer is (a).
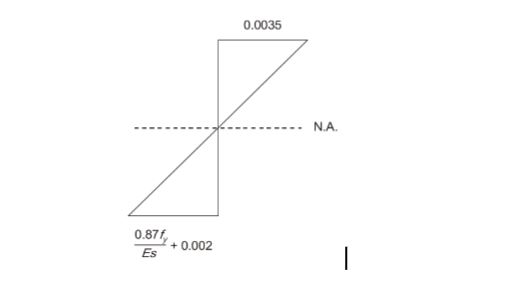
14.A singly reinforced concrete beam of balanced section is made of M20 grade concrete and Fe415 grade steel bars. The magnitudes of the maximum compressive strain in concrete and the tensile strain in the bars at ultimate state under flexure, as per IS 456: 2000 are ______, respectively. (round off to four decimal places)
(a) 0.0035 and 0.0038
(b) 0.0020 and 0.0018
(c) 0.0035 and 0.0041
(d) 0.0020 and 0.0031
Sol: (a)
Given data, Grade of concrete M-20 Grade of steel Fe-415
Balanced section, singly reinforced beam. As per Clause No. 38.1, IS 456 : 2000, Maximum strain in concrete at the outermost compression fibre = 0.0035 and
Strain in the tension reinforcement for balanced section at ultimate state under flexure
=0.002+ fy1.15Es=0.002+ 4151.152105=0.0038
- In cement concrete mix design, with the increase in water-cement ratio, which one of the following statements is TRUE?
(a) Compressive strength decreases but workability increase
(b) Compressive strength increases but workability decreases
(c) Both compressive strength and workability decrease
(d) Both compressive strength and workability increase
Sol: (a)
As the water-cement ratio increases, the porosity in the hardened concrete increases and hence the strength decreases. Also, as water-cement ratio increases, ducts higher water availability, the workability increases. Hence, correct answer is (a).
16.The specific gravity of a soil is 2.60. The soil is at 50% degree of saturation with a water content of 15%. The void ratio of the soil is _______ .
(a) 0.35
(b) 0.78
(c) 0.87
(d) 1.28
Sol: (b)
Gs = 2.60 S = 50% w = 15%
We know,
es=wGs
e × 0.5 = 0.15 × 2.60
e = 0.15× 2.60/ 0.5
e = 0.78
17.A group of 9 friction piles are arranged in a square grid maintaining equal spacing in all directions. Each pile is of diameter 300 mm and length 7 m. Assume that the soil is cohesionless with effective = 32°. What is the center-to-center′φfriction angle spacing of the piles (in m) for the pile group efficiency of 60%?
(a) 0.582
(b) 0.486
(c) 0.391
(d) 0.677
Sol: (b)
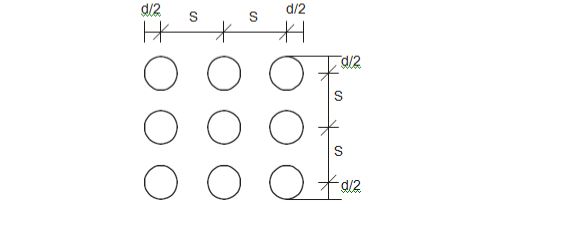
d = 300 mm L= 7 m C’ = 0 φ= 32° η group = 60% –
Centre to centre spacing =?
As the Nq value is not given, we can neglect the point bearing resistance and the pile capacity can be calculated using only the frictional capacity.
g=0.6= Block failure strengthIndividual pile strength
0.6= Kσ tanδ×4(2s+d)×79×σtanδk×πd×7 = 0.486m
18.A possible slope failure is shown in the figure. Three soil samples are taken from different locations (I, II and III) of the potential failure plane. Which is the most appropriate shear strength test for each of the sample to identify the failure mechanism? Identify the correct combination from the following options:
P: Triaxial compression test
Q: Triaxial extension test
R: Direct shear or shear box test
S: Vane shear test
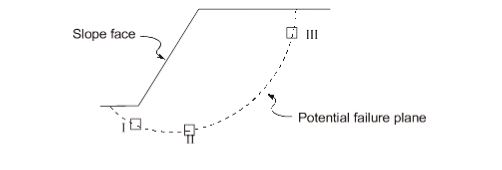
(a) I-Q, II-R, III-P
(b) I-R, II-P, III-Q
(c) I-S, II-Q, III-R
(d) I-P, II-R, III-Q
Sol: (a)
19.When a supercritical stream enters a mild-sloped (M) channel section, the type of flow profile would become _______
(a) M1
(b) M2
(c) M3
(d) M1 and M2
Sol: (c)
When super critical stream enters a mild (m) channel section, the type of flow.
Profile would be M3 or S1.
- Which one of the following statements is TRUE for Greenhouse Gas (CHG) in the atmosphere?
(a) GHG absorbs the incoming short wavelength solar radiation to the earth surface, and allows the long wavelength radiation coming from the earth surface to pass through.
(b) GHG allows the incoming long wavelength solar radiation to pass through to the earth surface, and absorbs the short wavelength radiation coming from the earth surface.
(c) GHG allows the incoming long wavelength solar radiation to pass through to the earth surface, and allows the short wavelength of radiation coming from the earh surface to pass through
(d) GHG allows the incoming short wavelength solar radiation to pass through to the earth surface, and absorbs the long wavelength radiation coming from the earth.
Sol: (d)
Green House Gas allow short wave radiation to pass through to the earth surface and absorbs the long wavelength radiation coming from the earth surface.
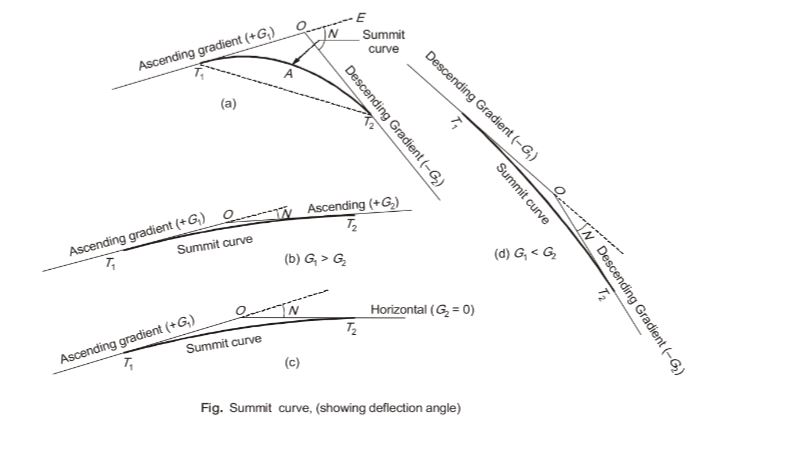
21.G1 and G2 are the slopes of the approach and departure grades of a vertical curve, respectively. Given |G1 | < |G2 | and |G1| ≠ |G2| ≠ 0
Statement 1: +G1 followed by +G2 results in a sag vertical curve.
Statement 2: –G1 followed by –G2 results in a sag vertical curve.
Statement 3: +G1 followed by –G2 results in a crest vertical curve. Which option amongst the following is true?
(a) Statement 1 and Statement 3 are correct; Statement 2 is wrong
(b) Statement 1 and Statement 2 are correct; Statement 3 is wrong
(c) Statement 1 is correct; Statement 2 and Statement 3 are wrong
(d) Statement 2 is correct; Statement 1 and Statement 3 are wrong
Sol: (a)
Given, |G1 | < |G2 | and |G1| |G2| 0
Statement 1: |G1 | < |G2 | This results in a vertical sag curve.
Statement 2: |G1 | < |G2 | This results in a vertical crest curve.
Statement 3: |G1 | < |G2 | This results in a vertical crest curve.
- The direct and reversed zenith angles observed by a theodolite are 56⁰00’00” and 303⁰00’ 00” respectively. What is the vertical collimation correction?
(a)+1⁰00’00”
(b)-1⁰00’00”
(c)-0⁰30’00”
(d)+0⁰30’00”
Sol: (d)
In above example of both direct zenith angle and reversed zenith angle are smaller than true value.
The error =1+2–3602=560+3030–3602 = -30’
So, correction = +0o 30’ 00”
23.a student is scanning his 10-inch X 10-inch certificate at 600 dots per inch (dpi) to convert it to raster. What is the percentage reduction in number of pixels if the same certificate is scanned at 300 dpi?
(a) 62
(b) 88
(c) 75
(d) 50
Sol: (c)
DPI = Dots Per Inch, it should be noted that DPI is not dots per square inch.
% reduction in number of pixels = 1060010600-100300103001060010600100
= 6002–30026002100 =75%
24.If M is an arbitrary real n × n matrix, then which of the following matrices will have non-negative eigenvalues?
(a)M2
(b) MMT
(c)MTM
(d) (MT)2
Sol: (b, c)
MX=λX ( is eigen value of M)
MMX= λMX
M2X=2X
2 is eigen value of M2
MX=λX
MTX=λX
MMTX=λMX
MMTX=(λX)=2X
MX=λX
MTX=λX
MTMX= λMX
MTMX=λX=2X
Positive Semidefinite Matrices: A matrix M is called positive semidefinite if it is symmetric and all its eigen values are non-negative then it is called a positive definite matrix. Now, if matrix M is real then MMT or MTM is positive semidefinite matrix so eigen values of MMT and MTM are real. Hence, option b, d are correct.
25.The following function is defined over the interval [–L, L]:
F(x) = px4 + qx5
If it is expressed as a Fourier series,
F (x) = ao + n=1ansin(πxL)+ bncos(πxL)
which options amongst the following are true?
(a) an, n = 1, 2, …, ∞ depend on p
(b) an, n = 1, 2, …, ∞ depend on q
(c) bn, n = 1, 2, …, ∞ depend on p
(d) bn, n = 1, 2, …, ∞ depend on q
Sol: (b, c)
bn= 1L–LLfxcos nπxL dx
bn depends on p
an=1L–LLfxsin (nπx)Ldx
an depends on q.
26.consider the following three structures

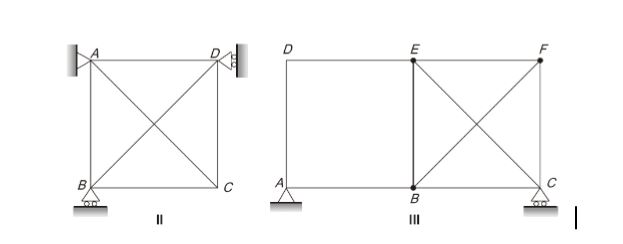
Structure I: Beam with hinge support at A, roller at C, guided roller at E, and internal hinges at B and D. L C A D B L
Structure II: Pin-jointed truss, with hinge support at A, and rollers at B and D.
Structure III: Pin-jointed truss, with hinge support at A and roller at C. Which of the following statements is/are TRUE?
(a) Structure I is unstable
(b) Structure II is unstable
(c) Structure III is unstable
(d) All three structures are stable
Sol: (a, b, c)
Structure I → Unstable Internal hinge at D can cause rigid body rotation.
Structure II → Unstable Since all reactions are concurrent at point A, rigid body rotation can take place.
Structure III → Unstable Even if m = 2j – 3 criteria is satisfied, there is an improper arrangement of members in 1st panel. Hence, shear in 1st panel is not resisted by any member. So, it is unstable.
27.Identify the waterborne diseases caused by viral pathogens:
(a) Acute anterior poliomyelitis
(b) Cholera
(c) Infectious hepatitis
(d) Typhoid fever
Sol: (a, c)
Water Borne Disease caused by (i) Bacterial— (a) Typhoid (b) Cholera
(ii) Virus— (a) Jaundice (Hapatitis virus) (b) Poliomyetitis
(iii) Protozoa— Amoebic dysentry
28.Which of the following statements is/are TRUE for the Refuse-Derived Fuel (RDF) in the context of Municipal Solid Waste (MSW) management?
(a) Higher Heating Value (HHV) of the unprocessed MSW is higher than the HHV of RDF processed from the same MSW.
(b) RDF can be made in the powdered form
(c) Inorganic fraction of MSW is mostly converted to RDF.
(d) RDF cannot be used in conjunction with oil.
Sol: (b)
(a) is false. The Higher Heating Value (HHV) of Refuse-Derived Fuel (RDF) processed from Municipal Solid Waste (MSW) is typically higher than the HHV of unprocessed MSW. This is because RDF processing removes non-combustible materials from MSW and concentrates the combustible fraction.
(b) is true. RDF can be produced in various forms including pellets, fluff, and powdered form. The form of RDF depends on the specific process and intended end use.
(c) is partially true. RDF processing typically removes a significant portion of the inorganic fraction of MSW, but not all of it. The remaining inorganic fraction is typically mixed with the RDF product.
(d) is false. RDF can be used as a fuel in a variety of combustion systems, including those that burn oil. In fact, RDF is often used as a supplemental fuel in cement kilns and other industrial processes that also use oil as a fuel.
29.The probabilities of occurrences of two independent events A and B are 0.5 and 0.8, respectively. What is the probability of occurrence of at least A or B (rounded off to one decimal place)? ________
Sol: (0.9)
P(A) = 0.5 P(B) = 0.8
Probability of occurence of atleast A or B = P(A ∩ B)
= 0.5 + 0.8 – P(A) × P(B)
= 0.5 + 0.8 – 0.5 × 0.8
= 1.3 – 0.4 = 0.9
30.In the differential equation dy + axy = 0 dx , a is positive constant. If y = 1.0 at x = 0.0, and y = 0.8 at x = 1.0, the value of a is _____ (rounded off to three decimal places).
Sol: 0.446 (0.445 – 0.447)
Given, dydx+αxy=0
dyv= -αxdx
ln y= – x22+C
Put y=1 at x=0
ln 1=0+C
C=0
ln y=- x22
Put y=0.8 at x=1
ln 0.8 = – 2
=0.4462
31.Consider the fillet-welded lap joint shown in the figure (not to scale). The length of the weld shown in the effective length. The welded surface meet at right angle. The weld size is 8 mm, and the permissible stress in the weld is 120 MPa. What is the safe load P (in kN, rounded off to one decimal place) that can be transmitted by this welded joint?
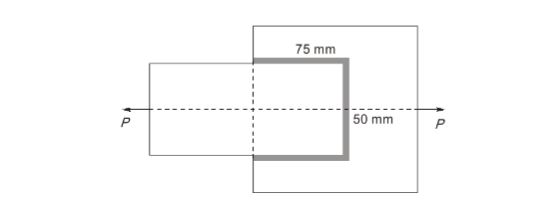
Sol: 134.4 kN (134 – 136)
Given data, Weld size = 8 mm Permissible stress = 120 MPa
Effective throat thickness, te = 0.7 × Weld size = 0.7 × 8 = 5.6 mm
Total effective length of weld, = 2 × 75 + 50 = 200 mm
Safe load ‘P’ in kN rounded upto one decimal⇒ palce = 5.6 × 200 × 120 × 10–3 = 134.4 kN.
32.A drained direct shear test was carried out on a sandy soil. Under a normal stress of 50 kPa, the test specimen field at shear stress of 35 kPa. The angle of internal friction of the sample is _____ degree (round off to the nearest integer).
Sol: 35
σn = 50 kPa, τf = 35 kPa
For sandy soil, C = 0
Shear stress = = C + tanφ
35 = 50tan φ
φ = 35°
33.A canal supplies water to an area growing wheat over 100 hectares. The duration between the first and last watering is 120 days, and the total depth of water required by the crop is 35 cm. The most intense watering is required over a period of 30 days and requires a total depth of water equal to 12 cm. Assuming precipitation to be negligible and neglecting all losses, the minimum discharge (in m3 /s, rounded off to three decimal places) in the canal to satisfy the crop requirement is ______.
Sol: 0.046 (0.045 – 0.047)
Area (A) = 100 ha
Total duration of irrigation = 120 days
Total depth of water required = 35 cm
Intense irrigation (A)
Time (BA) = 30 days
Depth of water (Δ) = 12 cm
Duty (D) = 8.64 B= 8.640.1230 = 2160 ha/cumec
Discharge required,
QA= AD=0.0463 m3/s
Remaining irrigation (B)
Duration = 90 days
Depth of water = 23 cm
Duty = 8.64 ×90 / 0.23 = 3380.87 ha/cumec
Discharge required (QB ) =
QB⇒ = 0.0296 m3 /s
Hence, minimum capacity required = 0.0463 m3 /s.
34.The ordinates of a one-hour unit hydrograph for a catchment are given below:
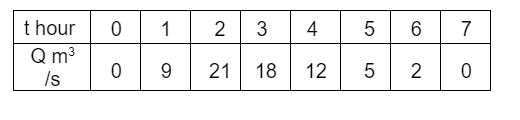
Using the principle of superposition, a D-hour unit hydrograph for the catchment was derived from the one-hour unit hydrograph. The ordinate of the D-hour unit hydrograph were obtained as 3 m3 /s at t = 1 hour and 10 m3 /s at t = 2 hour. the value of D (in integer) is _____.
Sol: 3 (3-3)
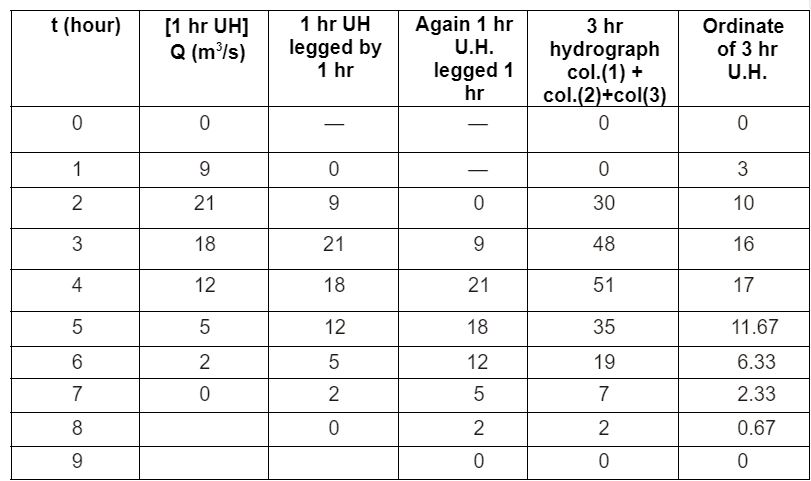
The duration D = 3 hours
35.For a horizontal curve, the radius of a circular curve is obtained as 300 m with the design speed as 15 m/s. If the allowable jerk is 0.75 m/s3 , what is the minimum length (in m, in integer) of the transition curve ? _____.
Sol: 15 m
Radius of circular curve (R) = 300 m
Vd = 15 m/s
Allowable jerk (C) = 0.75 m/sec3
Lmin= v3CR=1530.75300=15m
Minimum length of transition curve = 15 m.
Q.36 – Q.65 carry TWO mark each
36.A function f(x), that is smooth and convex-shaped between interval (x1 , xu ) is shown in the figure. This function is observed at odd number of regularly spaced points. If the area under the function is computed numerically, then _______.
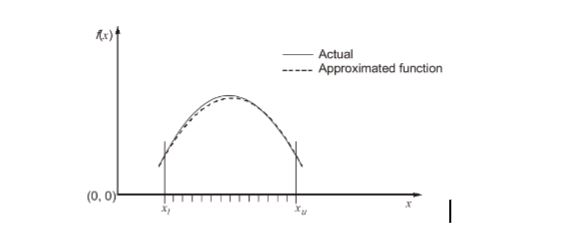
(a) the numerical value of the area obtained using the trapezoidal rule will be less than the actual.
(b) the numerical value of the area obtained using the trapezoidal rule will be more than the actual.
(c) the numerical value of the area obtained using the trapezoidal rule will be exactly equal to the actual.
(d) with the given details, the numerical value of area cannot be obtained using trapezoidal rule
Sol: (a)
Using the standard property of trapezoidal rule for converse shaped parabola, the numerical value of the area obtained using the trapezoidal rule will be less than the actual.
37.Consider a doubly reinforced RCC beam with the option of using either Fe250 plain bars or Fe500 deformed bars in the compression zone. The modulus of elasticity of steel is 2×105 N/mm2. As per IS456-2000, in which type(s) of the bars, the stress in the compression steel (fsc) can reach the design strength (0.87fy) at the limit state of collapse?
(a) Fe250 plain bars only
(b) Fe500 deformed bars only
(c) Both Fe250 plain bars and Fe500 deformed bars
(d) Neither Fe250 plain bars nor Fe500 deformed bars.
Sol: (a)
In a doubly reinforced beam, at the limit state of collapse. The strain in the extreme corression fibre will be 0.0035. As the compression reinforcement will be below this, the strain in if will be always less than 0.0035.
For Fe250, the yield strain
0.872502105=0.0010875
For Fe500, the yield strain =0.002+0.87fyEs
= 0.004175 > 0.0035
So, it is possible that Fe250 can reach upto its yield strain and hence can reach the design strength 0.87fy. Hence, correct answer is (a).
38.Consider the horizontal axis passing through the centroid of the steel beam cross-section shown in the figure. What is the shape factor (rounded off to one decimal place) for the cross-section?
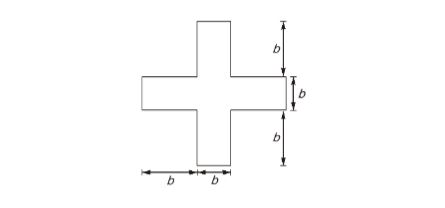
(a) 1.5
(b) 1.7
(c) 1.3
(d) 2.0
Sol: (b)
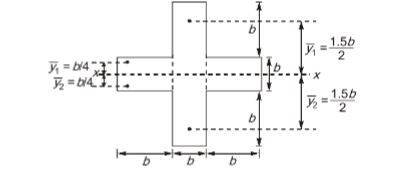
y1= 1.375b32.5b2=0.55b
ZP= A2y1+y2=2.75b3
Section Modulus
Z= IYmax=b(3b)312+2bb3123b2=1.611b3
Shape factor=ZpZe= 1.7
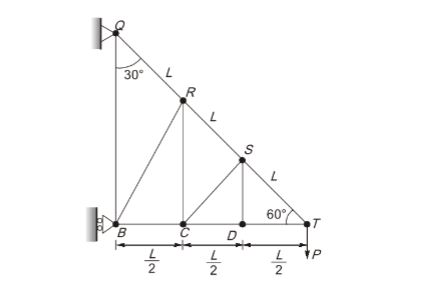
- Consider the pin-jointed truss shown in the figure (not to scale). All members have the same axial rigidity, AE. Members QR, RS, and ST have the same length L. Angles OBT, RCT, SDT are all 90°. Angles BQT, CRT, DST are all 30°. The joint T carries a vertical load P. The vertical deflection of joint T is PL k AE. What is the value of k?
(a) 1.5
(b) 4.5
(c) 3.0
(d) 9.0
Sol- b
At joint T,
∑Fy = 0
FTS sin60 = P
FTS = 2P3 (T)
∑Fx = 0
FTS cos60 = FDT
FDT = 2P3 (1/2) = P3 (C)
FTS = FSR = FRQ = 2P3 (T)
FDT = FCD = FBL = P3 (C)
Similarly,
KST = KSR = KRQ = 23 (T)
KDT = KCD = KBC = 13 (T)
VT = ∑PkLAE = 2P3 X 23 X L X 3AE + P3 X 13 X L2 X 3AE
VT = 4.5 PLAE
k = 4.5
40.With reference to the compaction test conducted on soils, which of the following is INCORRECT?
(a) Peak point of the compaction curve gives the maximum dry unit weight and optimum moisture content
(b) With increase in the compaction effort, the maximum dry unit weight increases
(c) With increase in the compaction effort, the optimum moisture content decreases
(d) Compaction curve crosses the zero-air-voids curve
Sol: (d)
Compaction curve crosses the zero-air-voids curve
41.Consider that a force P is acting on the surface of a half-space (Boussinesq’s problem). The expression for the vertical stress (σz) at any point (r, z) with the half-space is given as,
= 3P2z3r2+z22.5
where, r is the radial distance, and z is the depth with downward direction taken as positive. At any given r, there is a variation of σz along z, and at a specific z, the value of σz will be maximum. What is the locus of the maximum σz?
(a) z2 = 32 r2
(b) z3 = 32 r2
(c) z5 = 52 r2
(d) z3 = 52 r2
Sol: (a)
The expression for the vertical stress (σz) at any point (r, z) with the half-space is given as
= 3P2z3r2+z22.5
For z to be maximum
dzdz= 0
z2= 32r2
42.A square footing of size 2.5 m × 2.5 m is placed 1.0 m below the ground surface on a cohesion homogeneous soil stratum. Considering that the groundwater table is located at the base of the footing, the unit weights of soil above and below the groundwater table are 18 kN/m3 and 20 kN/m3 , respectively, and the bearing capacity factor Nq is 58, the net ultimate baring capacity of the soil is estimated as 1706 kPa (unit weight of water 10 kN/m3 ). Earlier, a plate load test was carried out with a circular place of 30 cm diameter in the same foundation pit during a dry season, when the water table was located beyond the plate influence zone. Using Terzaghi’s bearing capacity formulation, what is the ultimate bearing capacity (in kPa of the plate?
| |
|
Sol: (a)
For footing
qnu=1706 KPa
qnu=qNq–1+0.4 BN
N=(1706-1857)0.42.510=68
quplate=0.30.31868=110.16 KPa
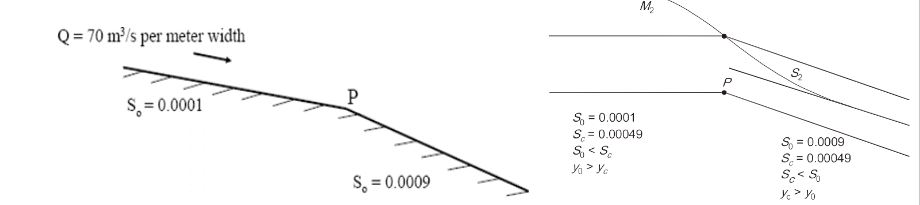
43.A very wide rectangular channel carries a discharge (Q) of 70 m3/s per meter width. Its bed slope changes from 0.0001 to 0.0009 at a point P, as shown in the figure (not to scale). The Manning’s roughness coefficient of the channel is 0.01. What water surface profile(s) exist(s) near the point P?
Q = 70 m3/s per meter width
| |
|
Sol: (a)
For a wide rectangular channel
R = AP = ByB+2y = Byb = y
Discharge per unit width, q is given by,
q = 1ny.y23.S12 = 1ny53.S12
calculation of Sc,
yc = q2g13
q = 1ny53.S12 = 1nq2g53.S12 = 1nq109g53S12
S12 = nqg59q109
S = ng59q192= 0.01 X 9.85970192 = 0.00049 (> 0.0001 and < 0.0009)
44.A jet of water having a velocity of 20 m/s strikes a series of plats fixed radially on a wheel revolving in the same direction as the jet at 15 m/s. What is the percentage efficiency of the plates? (round off to one decimal place).
| |
|
Sol: (a)
Given water jet velocity (V1) = 20 m/s
Wheel velocity (u) = 15 m/s
η=2u(V-U)V2×100=2×15×(20-15)202×100=37.5%
45.In the following table, identify the correct set of associations between the entries in Column-1 and Column-2.

|
|
|
|
Sol: (d)
- Reverse Osmosis – Concentration Polarization
- Trickling Filter – Ponding
- Coagulation– Charge
- Neutralization Adsorption- Freundlich Isotherm
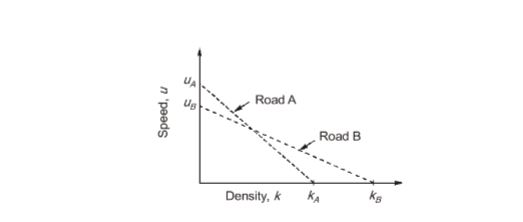
- A plot of speed-density relationship (linear) of two roads (Road A and Road B) is shown in the figure. If the capacity of Road A is CA and the capacity of Road B is CB , what is CACB?
|
|
|
|
Sol: (c)
For, Road ‘A’:
vf= uA, kj=kA
CA= UAKA4
For road B
vf= uB, kj=kB
CB= UBKB4
CACB= UAKAUBKB
- For the matrix
[A] = 1 2 3 3 2 1 3 1 2
Which of the following statements is/are TRUE?
- The eigenvalues of [A]T are same as the eigenvalues of [A]
- The eigenvalues of [A]–1 are the reciprocals of the eigenvalues of [A]
- The eigenvectors of [A]T are same as the eigenvectors of [A]
- The eigenvectors of [A]–1 are same as the eigenvectors of [A]
Sol: (a, b, d)
By standard properties:
- Eigen values of [A]T and [A] are same.
- Eigen vectors of [A] and [A]T are not same.
- Eigen values of [A]-1 is reciprocal of Eigen value of [A].
- Eigen vectors of [A]-1 are same as the eigenvectors of [A]
- For the function f(x)=ex|sinx|; x∈R, which of the following statements is/are TRUE?
- The function is continuous at all x
- The function is differentiable at all x
- The function is periodic
- The function is bounded
Sol: (a)
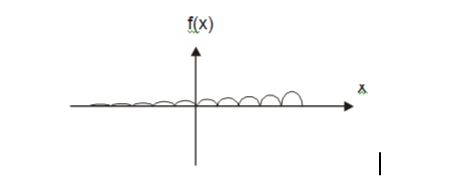
From above graph its clear that for every x Ꜫ R
f(x) = ex|sin x|
So, function is always continuous but in the graph there are corner points so function is not differentiable.
- Consider the beam shown in the figure (not to scale), on a hinge support at end A and a roller support at end B. The beam has a constant flexural rigidity, and is subjected to the external moments of magnitude M at one-third spans, as shown in the figure. Which of the following statements is/are TRUE?
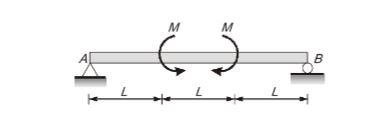
- Support reactions are zero
- Shear force is zero everywhere
- Bending moment is zero everywhere
- Deflection is zero everywhere
Sol: a, b
Using equilibrium equations
Ma=0
-M+M-Rb×3L=0
Rb=0
FV=0
Ra + Rb=0
Ra=0
- No shear force throughout the span.
- As there is BM in span CD, which leads to curvature in CD. i.e. deflection is not zero everywhere.
- Which of the following statements is/are TRUE in relation to the Maximum Mixing Depth (or Height) ‘Dmax’ in the atmosphere?
- Dmax is always equal to the height of the layer of unstable air
- Ventilation coefficient depends on Dmax
- A smaller Dmax will have a smaller air pollution potential if other meteorological conditions remain same
- Vertical dispersion of pollutants occurs up to Dmax
Sol: b and d
Maximum Mixing Depth (MMD)
- The dispersion of pollutants in the lower atmosphere is greatly aided by the convective and turbulent mixing that takes place.
- The vertical extent to which this mixing takes place depends on the environmental lapse rate which varies diurnally, from season to season and is also affected by topographical features.
- The depth of the convective mixing layer in which vertical movement of pollutants is possible, is called the maximum mixing depth (MMD).
- The ventilation coefficient is the product of mixing depth and the average wind speed
- Which of the following options match the test reporting conventions with the given material tests in the table?
Test reporting convention | Material test |
P.Reported as ratio | I.Solubility of bitumen |
Q. Reported as percentage | II. Softening point of bitumen |
R.Reported in temperature | III. Los Angeles abrasion test |
S.Reported in length | IV.Flash point of bitumen |
V. Ductility of bitumen | |
VI. Specific gravity of bitumen | |
VII. Thin film oven test |
- (P)-(VI); (Q) – (I); (R) -(II);(S)- (VII)
- (P)-(VI);(Q)-(III); (R) – (IV); (S) – (V)
- (P)-(VI); (Q)- (I); (R) – (II); (S) – (V)
- (P)-(VI);(Q)-(III); (R)- (IV); (S) (VII)
Sol: b, c
Solubility of bitumen: It is defined as weight of bitumen soluble in 100 ml of carbon disulphide.
Softening point of bitumen: It is the temperature at which bitumen attains a particular degree of softness.
Los angles abrasion test: It is reported as percentage of material finer than 1.7 mm with respect to total weight.
Flash point of bitumen: It is the lowest temperature at which bitumen catch five momentarily.
Specific gravity of bitumen is the ratio of mass of given volume of substance to the mass of equal volume of water, the temperature of both being specified. (P) – (VI); (Q) – (I, III, VII); (R) – (II, IV); (S) – (V).
- The differential equation,
dudt+2tu2=1
is solved by employing a backward difference scheme within the finite difference framework. The value of u at the (n−1)th time-step, for some n, is 1.75. The corresponding time (t) is 3.14 s. Each time step is 0.01 s long. Then, the value of (un – un – 1) is (round off to three decimal places).
Sol: –0.151 (-0.152 to -0.149)
Given DE:- dudt=ft,u=1-2tu2
By Euler’s backward method
Un = Un – 1 + hf(tn,Un)
Un = Un – 1 + h[1 – 2tnUn2]
Given, h = 0.01, Un-1 = 1.75, tn -1 = 3.14
So, tn = tn – 1 + h = 3.15
So, putting these values in (i)
Un = 1.75 + 0.01[1-2X3.15X Un2]
Un = 1.75 + 0.01 – 0.628Un2
62.8Un2 + 100Un + 175 = 0
Un = 1.599 and Un-1 = 1.75
We have Un – Un-1 = 1.599 – 1.75 = -0.151
- The infinitesimal element shown in the figure (not to scale) represents the state of stress at a point in a body. What is the magnitude of the maximum principal stress (in N/mm2 , in integer) at the point?
Sol: 7
yy= 6 N/mm2 and τxy = 3N/mm2
We know, =xx+yy2+xx–yy2cos2θ+xysin2θ
xx=-2N/mm2
Maximum Principal Stress 1=xx+yy2+xx–yy22+xy2
Maximum Principal Stress = 2 + 5 = 7 N/mm2
- An idealised bridge truss is shown in the figure. The force in Member U2L3 is ______ kN (round off to one decimal place).
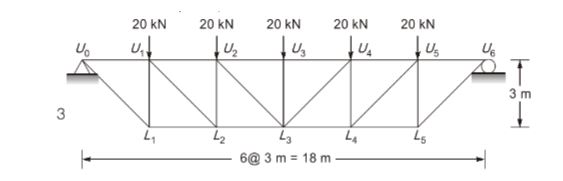
Sol: 14.1 (13.5 – 14.5)
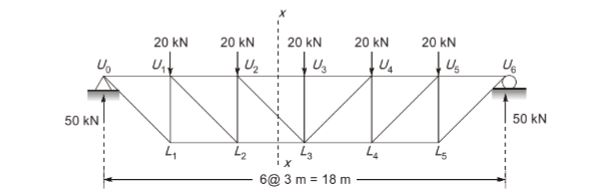
Vertical reaction at support at U0 and U6= 20 5 /2= 50kN
Applying method of sections and taking the section as shown
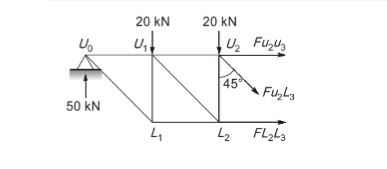
∑Fy = 0
FU2L3cos450 + 20 + 20 – 50 = 0
FU2L3 = 102kN =14.12 kN (tension)
- The cross-section of a girder is shown in the figure (not to scale). The section is symmetric about a vertical axis (Y-Y). The moment of inertia of the section about the horizontal axis (X-X) passing through the centroid is cm4 (round off to nearest integer).
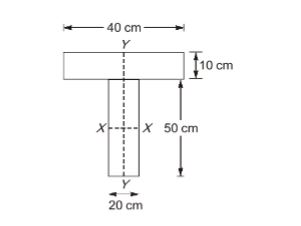
Sol: 468810 (464000 – 472000)
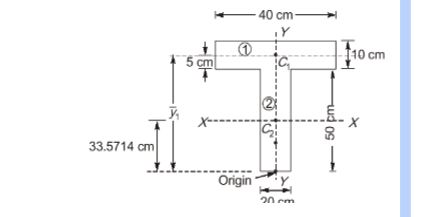
A1 = 40 X 10 = 400cm2
A2 = 20 X 50 = 1000 cm2
y1 = 50 + 5 = 55 cm
y2 = 50/2 = 25 cm
Centroid of composite shape, from bottom,
y = A1y1+A2y2A1+A2 = 400X55+(1000X25)400+1000 = 33.5714cm
IXX = 40 X 10312+400(y1– y)2 + 20 X 50312+1000(y– y2)2
= 187007.2925 + 281802.2313 = 468810 cm4
- A soil having the average properties, bulk unit weight = 19 kN/m3; angle of internal friction = 25° and cohesion = 15 kPa, is being formed on a rock slope existing at an inclination of 35° with the horizontal. The critical height (in m) of the soil formation up to which it would be stable without any failure is (round off to one decimal place). [Assume the soil is being formed parallel to the rock bedding plane and there is no ground water effect.] [
Sol: 5.0 (4.8 – 5.2)
C+γHccos2βtanϕ = γHcsinβcosβ
15 + 19 X HC X cos235otan25o = 19 X HC X sin35o cos35o
HC=5.03 m
57. A smooth vertical retaining wall supporting layered soils is shown in figure. According to Rankine’s earth pressure theory, the lateral active earth pressure acting at the base of the wall is kPa (round off to one decimal place).
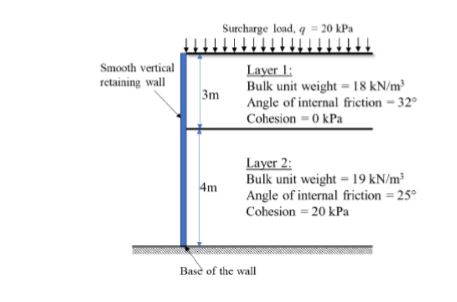
Sol: 35.4 (34.0 – 37.0)
H=KAV-2CKa
Ka= 1-sin251+sin25=0.408
H=35.7KPa
- A vertical trench is excavated in a clayey soil deposit having a surcharge load of 30 kPa. A fluid of unit weight 12 kN/m3 is poured in the trench to prevent collapse as the excavation proceeds. Assume that the fluid is not seeping through the soil deposit. If the undrained cohesion of the clay deposit is 20 kPa and saturated unit weight is 18 kN/m3 , what is the maximum depth of unsupported excavation (in m, rounded off to two decimal places) _____?
Sol: 3.33 (3.30 – 3.35)
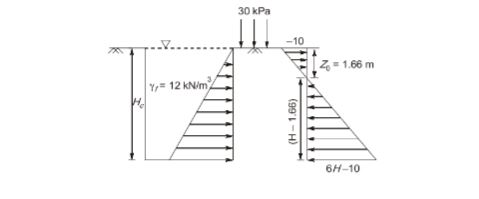
Now, active pressure at depth
z=kaγz-2CKa-12z+kq
At z=0
z= -10KN/m2
At z0,z=0
6z0-10=0
z0=1.66 m
At depth H,
H=kaγz-2CKa-12H+Kq=6H-10
For unsupported depth of excavation, total active thrust must be zero.
So, ½ ×10×1.66=1/2 ×(H-1.66) (6H-10)
H=10/3=3.33m
- A 12-hour storm occurs over a catchment and results in a direct runoff depth of 100 mm. The time distribution of the rainfall intensity is shown in the figure (not to scale). The ϕ-index of the storm is (in mm, rounded off to two decimal places) _______.
Sol: 3.60 (3.59 – 40.1)
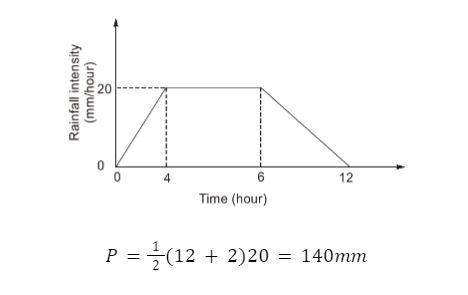
W index=P-Rt=3.33mm/hr
=Pe-Rt=3.60mm/hr
NOTE: this question is challengable since index unit is mm/hr not mm.
- A hydraulic jump occurs in a 1.0 m wide horizontal, frictionless, rectangular channel, with a pre-jump depth of 0.2 m and a post-jump depth of 1.0 m. The value of g may be taken as 10 m/s2. The values of the specific force at the pre-jump and post-jump sections are same and are equal to (in m3, rounded off to two decimal places) _____________
Sol: 0.62 (0.60 to 0.64)
Given, B = 1 m = width of channel
Pre-jump depth = y1 = 0.2 m Post-jump depth = y2 = 1.0 m
As we know, Specific force=Fs=F1+M1ρg
yc3=y1y2(y1+y2)2=0.12
q2g=0.12
Q2=q2B2=1.2212=1.2
Fs=1×0.2×0.22+1.210×1×0.2=0.62 m3/m
- In Horton’s equation fitted to the infiltration data for a soil, the initial infiltration capacity is 10 mm/h; final infiltration capacity is 5 mm/h; and the exponential decay constant is 0.5 /h. Assuming that the infiltration takes place at capacity rates, the total infiltration depth (in mm) from a uniform storm of duration 12 h is ________. (round off to one decimal place)
Sol: 70.0 (69.7 – 70.1)
Given, fo = 10 mm/hr, fc = 5 mm/hr, k = 0.5 /hr
∴ Total infiltration =0125+(10-5)e-05tdt =59.97+10=69.97 mm
- The composition and energy content of a representative solid waste sample are given in the table. If the moisture content of the waste is 26%, the energy content of the solid waste on dry- weight basis is MJ/kg (round off to one decimal place).
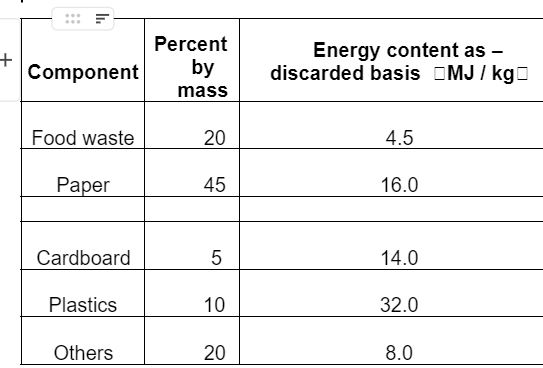
Sol:18.4 (18 – 19)
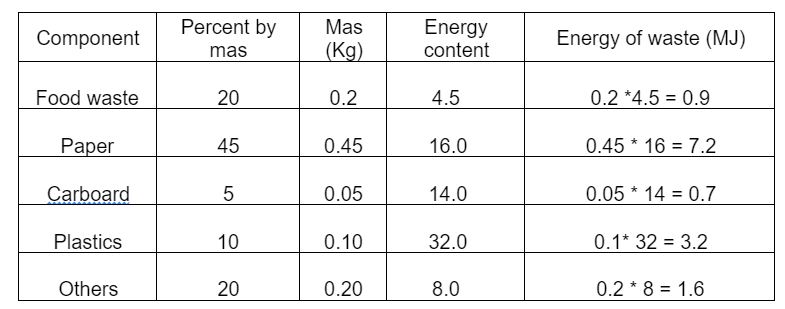
Energy content = 0.9 + 7.2 + 0.7 + 3.2 + 1.6 = 13.6 MJ/kg
Energy content for moisture content of 26%:
= 13.6/(100-26)% = 18.38 MJ/kg = 18.4 MJ/kg
- A flocculator tank has a volume of 2800 m3. The temperature of water in the tank is 15°C, and the average velocity gradient maintained in the tank is 100/s. The temperature of water is reduced to 5 C, but all other operating conditions including the power input are maintained as the same. The decrease in the average velocity gradient (in %) due to the reduction in water temperature is (round off to nearest integer). [Consider dynamic viscosity of water at 15°C and 5°C as 1.139 × 10–3 N-s/m2 and 1.518 × 10–3 N-s/m2, respectively]
Sol: 13 (12 – 15)
Case I: T1 = 15°C
P1=G121V
Case 2
T2 = 5⁰C
P2=G22×1.518×10-3V
Power is same in both cases
⟹G1G2=1.154
Percent decrease= G1–G2G1×100=13%
- The wastewater inflow to an activated sludge plant is 0.5 m3/s, and the plant is to be operated with a food to microorganism ratio of 0.2 mg/mg-d. The concentration of influent biodegradable organic matter of the wastewater to the plant (after primary settling) is 150 mg/L, and the mixed liquor volatile suspended solids concentration to be maintained in the plant is 2000 mg/L. Assuming that complete removal of biodegradable organic matter in the tank, the volume of aeration tank (in m3, in integer) required for the plant is ______.
Sol: 16200
Sol. Given, Q= 0.5 m3/sec
F/M=0.2mg/mg-day
S0=150mg/L
X=2000mgL
FM=QS0Vx
0.2=0.5×86400×150V×2000
V=16200m3
- Trigonometric levelling was carried out from two stations P and Q to find the reduced level (R. L.) of the top of hillock, as shown in the table. The distance between Stations P and Q is 55 m. Assume Stations P and Q, and the hillock are in the same vertical plane. The R. L. of the top of the hillock (in m) is _____ (round off to three decimal places
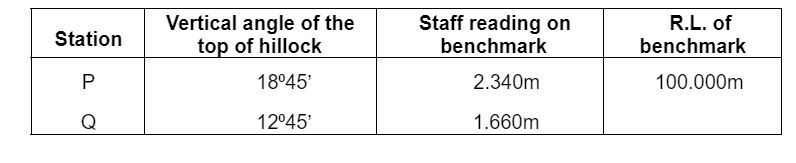
Sol: 137.627 (137.500 – 137.700)
We have, tan12°45’ = V+0.68D+55
Tan 18045‘=VD
On solving (i) and (ii), we get V = 35.287 m D = 103.954 m
Now, R.L of hill top = R.L of BM + 2.34 + V = 100 + 2.34 + 35.28 = 137.627m
